Lecture 9: Supervised learning

STAT598z: Intro. to computing for statistics

Vinayak Rao

Department of Statistics, Purdue University

Supervised learning

We are given training data $(X, Y) = \{(x_1, y_1 ),\cdots , (x_N, y_N )\}$

  • X: independent variables, inputs, predictors, features
  • Y: dependent variables, outputs, response

$x \in \mathbb{R}^P$ (usually)

  • regression: $y \in \mathbb{R}$
  • classification: $y \in \{0, 1\}$
  • structured prediction: More complicated high-dimensional spaces with dependent components (e.g. the space of images or sentences)

We assume $y_i = f(x_i ) + \varepsilon_i$

$\varepsilon$ is noise (includes randomness and approximations)

  • Independently and identically distributed (i.i.d.) according to some probability distrib. (e.g. Gaussian)

Given the training set $(X, Y)$, we want to estimate $f$:

  • to study the relation between x and y
  • to make predictions of y’s for unobserved x’s

Good predictors can be hard to interpret

Parametric learning

Index functions $f$ by a finite-dimensional parameter vector

E.g. linear regression

  • Parameters are coefficients of a hyperplane
  • Parameters have a clear interpretation
  • Can be a bad approximation of reality

Linear regression

via the lm function in R

In [ ]:
library('ggplot2')
DataIncm <- read.table('Data/Income2.csv',header=T,sep=',')
ggplot(DataIncm) + geom_point(aes(x=Education,y=Income))
In [ ]:
fit <- lm(Income ~ Education, DataIncm); fit

The first argument is a formula

  • takes the form response ~ predictors
  • response is a linear combination of predictors
  • above we have just one predictor: $Education$
  • $Income = \beta_1 \cdot Education + \beta_0 + \epsilon$

Second argument unnecessary if variables in formula exist in current environment

See documentation for other optional arguments

Can print fit:

In [ ]:
fit

This is not all the information in fit (why?)

  • Try typeof(), class(), str()
  • Try plotting it
In [ ]:
print.default(fit)

Observe fit contains the entire dataset!

Can disable with model = FALSE option

Can directly plot with ggplot :

In [ ]:
plt1 <- ggplot(DataIncm, aes(x=Education, y = Income)) +
          geom_point(size=2, color='blue') +
          theme(text=element_text(size=10))
In [ ]:
plt1 + geom_smooth(method='lm', se=FALSE, #Disable std. errors
                   color='magenta', size=2)

Can regress against Seniority

In [ ]:
fit <- lm(Income ~ Seniority, DataIncm)

Can regress against both Education and Seniority

In [ ]:
fit <- lm(Income ~ Education + Seniority, DataIncm)
  • + does not mean input is sum of Educ. and Sen.

Rather: $Income = \beta_2 \cdot Seniority + \beta_1 \cdot Education + \beta_0 + \varepsilon$

For the former, use I:

fit <- lm(Income ~ I(Education + Seniority), DataIncm)

  • $Income = \beta_1 \cdot (Seniority + Education) + \beta_0 + \varepsilon$

Prediction

In [ ]:
fit <- lm(Income ~ Education + Seniority, DataIncm)

How do we make predictions at a new set of locations? E.g. (15, 60) and (20, 160)?

In [ ]:
pred_locn <- data.frame(Education=c(15,20), Seniority= c(60,160))
predict.lm(fit, pred_locn)
In [ ]:
edu_pred <- 10:25
sen_pred <- seq(0,200,10)
pred <- data.frame(Education=rep(edu_pred, length(sen_pred)),
               Seniority=rep(sen_pred, each=length(edu_pred) ))
p_val <- predict.lm(fit, pred)
pred$p_val = p_val
In [ ]:
plt <- ggplot(DataIncm, aes(x=Education, y=Seniority, 
                          color=Income))+
    geom_tile(data=pred, aes(x=Education, y=Seniority, 
                                  color=p_val, fill=p_val)) +
    geom_point(size=1) + theme(text=element_text(size=10)) +
    scale_color_continuous(low='blue', high='red') +
    scale_fill_continuous(low='blue', high='red') +
    geom_point(shape=1,size=1,color='black') + 
      guides(fill=FALSE) # Remove legend for 'fill'
In [ ]:
plt

Specifying a model for lm

Symbol Meaning Example
+ Include variable x + y
: Interaction between vars x + y + z + x:z + y:z
* Variables and interactions (x + y) * z
^ Vars and intrcns to some order (x + y + z)^3
- Delete variable (x + y + z)^3 - x:y:z
poly Polynomial terms poly(x,3) + (x + y) * z
I New combination of vars I(x*y + z)
1 Intercept x - 1

See documentation and http://ww2.coastal.edu/kingw/statistics/R-tutorials/formulae.html

Generalized linear model

A linear model with Gaussian noise is often inappropriate. E.g.

  • response is always positive
  • count valued response
  • {0, 1} or binary-valued as in classification

A better model might be:

$ response = g (\sum_{i=1}^N \beta_i \cdot predictor_i) + \varepsilon$

$g$ is a ‘link’ function, $\varepsilon$ is no longer Gaussian

Can fit in R with glm() (see documentation)

Nonparametric methods

No longer limit yourself to a parametric family of functions

Much more flexible

Often much better prediction

Complexity of $f$ can grow with size of dataset

Often hard to interpret

k-nearest neighbors

Given training data $(X, Y)$

Given a new $x^∗$ , what is the corresponding $y^∗$?

Find the k-nearest neigbours of $x^∗$ . Then:

  • Classification: Predicted $y^∗$ is the majority class-label of the neighbors
  • Regression: Predicted $y^∗$ is the average of the $y$’s of the neighbors

3-nearest neighbors

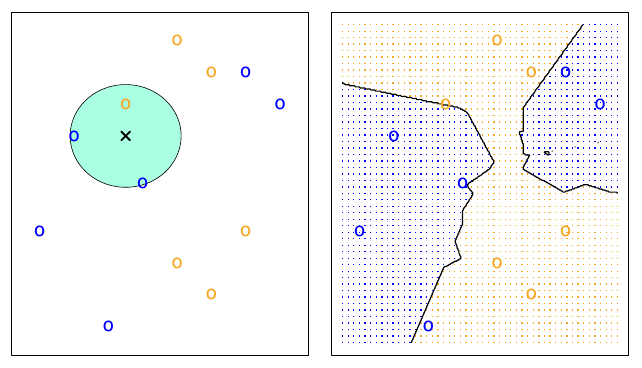Alt text (*An Introduction to Statistical Learning*, James, Witten, Hastie and Tibshirani)

Complexity of decision boundary grows with size of training set: ‘Nonparametric’

Pros:

  • Very intuitive computational algorithm.
  • Very easy to ‘fit’ data (you don’t, you just store it)
  • Tends to outperform more complicated models.
  • Easy to develop more complicated extensions E.g. locally-adaptive kNN.
  • Exists theory for such models.

Cons:

  • Cost of prediction grows linearly with training set size (can be expensive for large datasets)
  • Tends to break down in high-dimensional spaces.
  • Exempler-based approaches are hard to interpret.

10-nearest neighbors

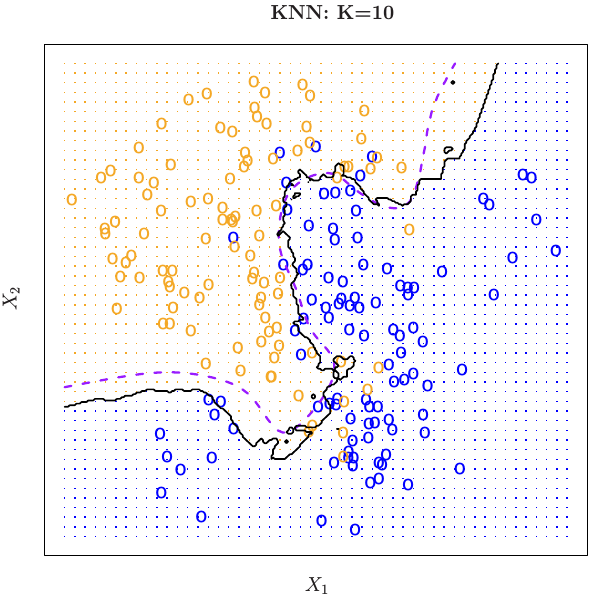Alt text (*An Introduction to Statistical Learning*, James, Witten, Hastie and Tibshirani)

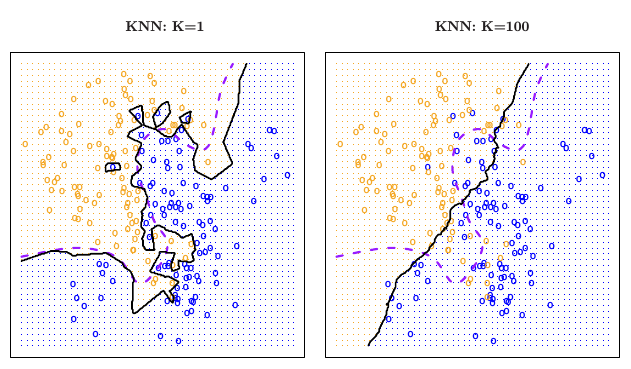Alt text (*An Introduction to Statistical Learning*, James, Witten, Hastie and Tibshirani)

  • What distance function do we use? Typically Euclidean.
  • What k do we use? Typically 3, 5, 10

Usually chosen by cross-validation (more later)

Large k: smooth decision boundary

Small k: complex decision boundary (with local variations)

  • k is a measure of model-complexity

How do we perform model selection?

Do we prefer simple or complex models?

Bias-variance trade-off

Overly simple models

  • cause underfitting (or bias)
  • ignore important aspects of training data

Overly complex models

  • cause overfitting (or variance)
  • can be overly sensitive to noise in training data

Complex models reduce training error, but generalize poorly.

Cross-validation

How do we estimate generalization ability? Create an unseen test dataset.

Cross-validation:

  • Split your data into two sets, a training and test dataset.
  • Fit all models on training set.
  • Evaluate all models on test set.
  • Pick best model.

Choosing k by cross-validation

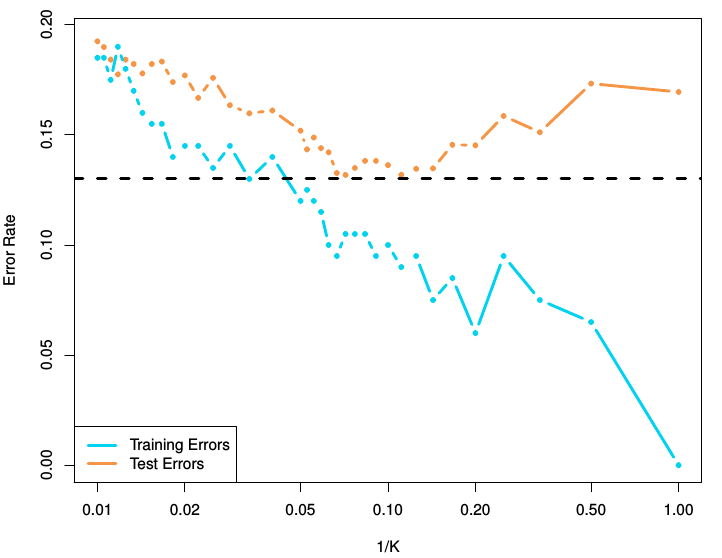
Alt text

Often 50-50 or 70-30 training-test splits are used

Too small a test set:

  • Noisy estimates of generalization error

Too small a training set:

  • Wasting training data
  • Model selected using small training set may be simpler that model relevant to the entire training set

k-fold crossvalidation

Split your data into k-blocks.

For i = 1 to k:

  • Fit algorithm on all except block i.
  • Test algorithm on block i. Overall generalization error is the average of all errors.
  • Can use larger training sets
  • Can get confidence intervals on generalization error.

k = N: leave-one-out cross-validation

k-fold crossvalidation

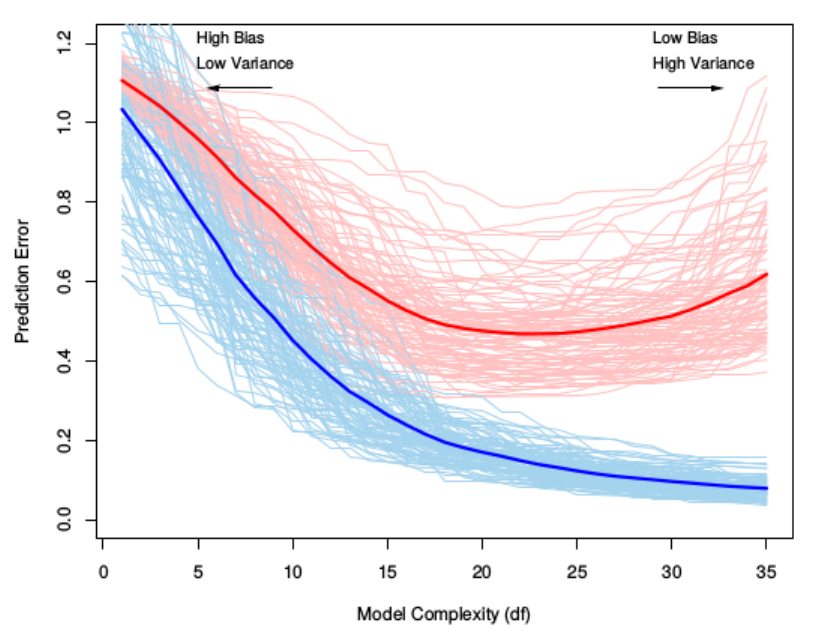Alt text (*An Introduction to Statistical Learning*, James, Witten, Hastie and Tibshirani)